لقاء في پودكاست ريد روز مع الأستاذ أحمد الجوهري

 Red Rose podcast 

بعنوان‫: تاريخ موجز للكون بنء علي الفيزياء والمنهجية العلمية

 (Recorded: July 22, 2023. Published: July 24, 2023)

Soundcloud

Spotify 

Google podcast 

Castbox 

My book "Covariant Physics: From Classical Mechanics to General Relativity and Beyond"

 

Covariant Physics made it to the Best General Relativity Books of All Time

 

 

 

I'm happy to announce that my book, "Covariant Physics: From Classical Mechanics to General Relativity and Beyond", made it to BookAuthority's Best General Relativity Books of All Time:
https://bookauthority.org/books/best-general-relativity-books?t=edusem&s=award&book=0198864892 

BookAuthority collects and ranks the best books in the world, and it is a great honor to get this kind of recognition. Thank you for all your support!

The book is available for purchase on Amazon.

الزي الأكاديمي

6-4-2016

الپوست الأصلي علي الفيسبوك‫:

https://www.facebook.com/moataz.emam.007/posts/pfbid0yfWkFZRqjwruv126FLgjktNbJsLrBrQBjuD1osb9ySwvW52gcjW212zTTHUQ7GDUl

 

الزي الأكاديمي له تاريخ طويل يعود إلي زي كهنة الكنيسة في العصور الوسطي ، لأنه يرمز إلي العلم والتعليم ، والكهنة في تلك الأوقات كانوا الوحيدين المتعلمين القادرين علي القراءة والكتابة. ويقال ايضاً انه مستوحى من زي العرب التقليدي لانهم اول من نشأ مراكز للعلم بصورتها الحديثة. بمرور الوقت وظهور العلم الغير ديني تحول الزي إلي رمز العلم والتعلم الجامعي تحديداً. وأصبح في كثير من الجامعات الأوروپية زياً للأستاذ الجامعي فقط يرتديه يومياً وليس فقط في المناسبات (لا يزال البعض يفعلون ذلك في إنجلترا وأذكر إن أحد أساتذتنا في قسم الرياضيات بكلية علوم القاهرة كان يرتديه يومياً وكان الوحيد الذي يفعل ذلك في وقتها). بمرور الوقت إكتسبت الوان وأشكال الزي الأكاديمي معاني مختلفة تختلف من دولة إلي دولة. الولايات المتحدة مثلاً لها رموز في الزي مأخوذة من جامعة أكسفورد بإنجلترا. كمثال شكل كم الروب ، لو بيضاوي يكون المرتدي حاصل علي البكالوريوس ، لو مدبب ماجستير ، ومفلطح عادي دكتوراه. لون الشرشوبة في القبعة أسود للبكالوريوس والماجستير وذهبي فقط للحاصل علي الدكتوراه ، وترتدي الشرشوبة علي يمين الوجه قبل التخرج وتنقل إلي اليسار بعد الحصول علي الدرجة. أما الوان الزي فتختلف بإختلاف المجال العلمي لمرتدي الزي ، وأيضاً ألوان الجامعة التي تخرج منها. وهكذا. كمثال هذا هو الزي الذي أرتديه في المناسبات:

 

 

هو أنا بعمل أبحاث في إيه‫؟

4-30-2022

الپوست الأصلي في فيسبوك‫:

https://www.facebook.com/moataz.emam.007/posts/pfbid0mhbKuoqrt3H9S4TWQ2RNu7KsgRF8f9XHE5u44NDkCcvVJGTNoAt1v7VoVCZr6JFPl

 بعض الأصدقاء بيسألوني عن الأبحاث بتاعتي وأنا بعمل إيه بالظبط فقلت أعمل بوست أدي ملخص بسيط‫.‫ 

أنا بشتغل في نظرية الأوتار الفائقة ‫، تحديداً في السوپر جراڤيتي Supergravity إلي هي نظريات تعتبر حالة خاصة من الأوتار في طاقة منخفضة نسبياً‫ ‫، وفيها تركيز أعلي علي جانب الجاذبية من نظرية الأوتار ‫، الجانب إلي بحبه ومألف كتاب فيه‫‫.‫ ميزة العمل في هذا الجانب من نظرية الأوتار إن فيه شواهد في النظرية لا تظهر إلا في الnonperturbative regime إلي هو الrange إلي نقدر نقول إنه أوتار في حالة طاقة منخفضة‫.‫ وهذه النظريات تعتمد بالأساس علي النسبية العامة زائد ما يسمي بالتناظر الفائق supersymmetry في أبعاد أعلي من الأربعة إلي إحنا عايشين فيهم‫.‫ شغل الدكتوراه بتاعي مثلا كان في M-theory في حالة سوپرجراڤيتي في أحد عشر بعداً‫.‫ ثم بعد الدكتوراه لفت إنتباهي نظرية سوپرجراڤيتي في خمس أبعاد محدش بيشتغل فيها غير حفنة من الناس ‫، النظرية عجبتني لأكتر من سبب ‫، منهم إن محتوي المجالات إلي فيها يحمل ثراء رياضي كبير جداً وفي رأيي لم يستغل بعد‫.‫ ده غير إنها مرتبطة في رأي إرتباط وثيق بأليات تخفيض الأبعاد الزيادة وعلاقتها بالطبولوجي بتاعتها‫.‫ علشان كدة نقدر نقول تخصصت فيها إلي حد ما فترة طويلة ‫، البحث إلي تحت ده أنا بتصور إنه أهم بحث أنا كتبته في حياتي علي الإطلاق ‫، لأن فيه بعيد صياغة النظرية بإستخدام ثراءها التناظري في حاجة إسمها symplectic space ‫، لأن لفت نظري إن بالرغم إن هذا الثراء معروف من قبل ولكن محدش إستغله‫.‫ فطورت طريقة رياضية بسيطة كدة لإستغلاله ‫، وبعد كدة نشرت كذا بحث بستخدم فيه طريقتي دي لإثبات إنها فعلاً بتسهل الشغل‫.‫ لقيت بعض هذه النتائج فيها حاجات دمها خفيف زي أكوان أخري مثلاً‫ وأيضاً تفسيرات محتملة لتسارع الكون بتاعنا سواء في مرحلة التضخم الأولي inflation أو في المرحلة الحالية‫.‫

 

تلاحظ إن العنوان فيه كلمة covariance وكتابي أيضاً عن موضوع الcovariance ‫(‫لكن نوع مختلف عن إلي في البحث ده‫)‫‫.‫ نقدر نقول كدة إن موضوع الكوڤاريانس ده عاجبني ‫، بجد فيه جمال رياضي منقطع النظير ‫، في أي صورة من صوره‫.‫

ماعلينا ‫، أديني أهو رديت علي سؤال الأصدقاء مع إني عارف كويس إني بتكلم في صيغة طلاسم لمعظم الناس‫.‫ طيب هو أبحاثي دي فايدتها إيه ولا ليها تطبيقات ولا حنكسب منها أي حاجة قريب‫؟ الإجابة هاهاهاهاهاهاهاهاهاهاها قطعاً لأ ‫، دي سيادتك تسالي نظرية جوة تسالي نظرية من جوة نظريات محدش عارف بتصف الطبيعة أم لا‫.‫ طيب بتشتغل فيها ليه يا معتز لما هي كدة‫؟ الإجابة‫: مزاج عندي 

 

صحيح فعلاً ‫، أنا مش بعمل حاجة في حياتي علشان حتكسبني فلوس ولا حتجيبلي نوبل ولا حتي حتديني citation عالي ‫، أنا بعمل أبحاث علشان عاجبني المواضيع دي‫.‫ العمر أقصر من إني أضيعه في حاجة مش بحبها‫.‫

 

 https://arxiv.org/abs/0904.1951

 

 

العلم والفلسفة ، خناقة حقيقية ولا مفتعلة؟

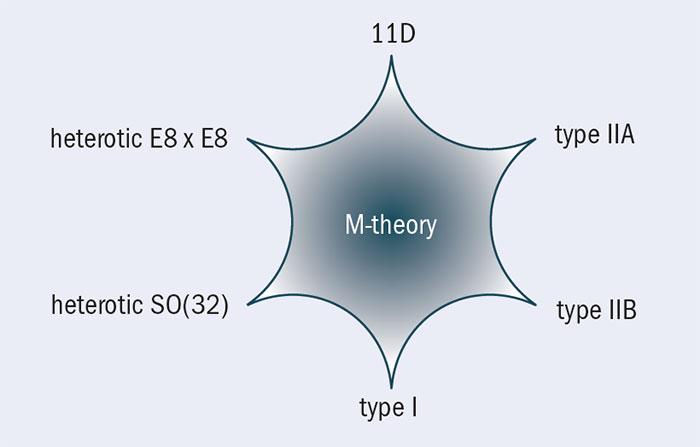
 هذ اللقاء كان من الأهمية بحيث أفردت له تدوينة خاصة بدلاً من إضافته علي قائمة اللقاءات‫.‫ تشرفت فيه بالأساتذة‫ ‫(‫بلا ترتيب محدد‫)‫:
دكتور نسيم مجدي ‫، دكتور محمد الشمري ‫، دكتور حسن عيسي ‫، دكتور رياض المشاء ‫، دكتور طارق السرحان ‫، دكتورة نشوي إسماعيل ‫، دكتور محمد بركات‫.‫

ينقسم الحوار الذي إستمر أربع ساعات إلي ثلاثة أجزاء عظمي:

حوار عام بين جميع المشاركين من الأول ولمدة ساعة تقريباً‫.‫

حوار بين دكتور طارق السرحان ودكتور حسن عيسي 

حوار بين دكتور طارق السرحان ودكتور محمد بركات‫.‫

Maxwell’s Theory of Electromagnetism. A Concise Summary for Aliens

 An article for undergraduate physics majors on the compactness of Electrodynamics and how it inspires the unification of physics.

https://www.scribd.com/document/641646675/Maxwell-s-Theory-of-Electromagnetism-A-Concise-Summary-for-Aliens

 

 

تعالوا نتكلم عن السمترية - مجموعة مقالات فيسبوك

5-30-2022

تعالوا نتكلم عن السمترية -الجزء الأولاني

 

من أجمل الأساسيات في الفيزياء وأكترها أهمية مبدأ التناظر ‫، أو السمترية ‫، خلينا نستعمل المصطلح الأصلي 

 

Symmetry سمترية

 

المبدأ بصفة عامة معناه إيه‫؟ معناه كالأتي‫:

تصور وجود معادلات بتوصف ظاهرة فيزيائية معينة‫.‫ إعمل في المعادلات دي حاجة ‫، يعني مثلاً إضربها في رقم ‫، أو إجمع عليها رقم ‫، أو أخضعها لعملية رياضية معقدة أكتر من مجرد الضرب في رقم أو جمع رقم‫.‫ لو لقيت بعد الحركة دي إن نفس المعادلات بتطلعلك تاني من غير أي فيزياء جديدة بتظهر فيها يبقي سيادتك لقيت سمترية‫.‫ خلي بالك الأرقام ممكن تختلف لكن الظواهر الفيزيائية هي هي‫.‫

السمتريات أنواع مختلفة ‫، أول نوع بنسميه سمترية الزمكان‫.‫

 

Spacetime symmetry

 

ودي بتنقسم لأنواع ‫، مثلاً عندك 

 

time translation symmetry

 

يعني لو شلت الزمن وبدلته بزمن تاني بس مضاف عليه رقم

 

t → t + a

 

حيث a ده رقم ثابت تطلعلك نفس النتيجة الفيزيائية‫.‫ يعني إيه‫؟ يعني كأن المعادلة بتقولك لو عملت التجربة النهاردة أو بكرة أو بعده أو كنت عملتها إمبارح أو السنة إلي فاتت حتديك نفس النتيجة الفيزيائية‫.‫

وسمترية المكان كمان نفس الشيء ‫، إنك لو شلت المكان وحطيت مكانه أي حاجة تانية حيديك نفس النتيجة 

 

x → x + b

 

‫حيث b ده رقم ثابت برضه ، بمعني إن المعادلة بتقولك لو عملت التجربة في بيتكوا ولا عندي ولا علي القمر ولا في مجرة أندروميدا حتديك نفس النتيجة‫.‫ تاني‫: ممكن الأرقام تختلف لكن الظاهرة الفيزيائية حتطلع هي هي‫.‫

أخر نوع من أنواع سمتريات الزمكان هو سمترية الدوران

 

rotational symmetry

 

إلي بتقولك إنك لو أخدت التجربة ودورتها في الفراغ بأي درجة برضه حتديك نفس النتيجة ‫(‫‫المعادلة معقدة أكتر من إلي فوق)‫‫.‫ خلي بالك إنك لازم تاخد كل العوامل إلي التجربة بتعتمد عليها وتدورها معاك‫.‫ يعني لو التجربة بتعتمد علي مجال الجاذبية مثلاً يبقي لازم تدور الكوكب كله معاك‫.‫ ودي بسيطة ‫، خد التجربة من مصر وإعملها في الصين‫.‫

السمتريات الزمكانية دي سهلة وفي نفس الوقت منطقية جداً‫.‫ السمتريات دي عادةً بتعتمد علي تطبيقها علي المعادلات التفاضلية للظاهرة ‫، زي معادلات الحركة لنيوتن أو معادلات المجال وماكسويك وهلم جرة‫.‫

الموضوع بيزداد تعقيداً ‫، يعني مثلاً السمتريات إلي فوق دي إسمها

 

Global symmetries

 

يعني إيه‫؟ يعني إنت لما بتغير مثلاً

 

x → x + b

 

إنت بتعمل كدة في كل x في أي مكان في الفراغ مرة واحدة تضيف عليه رقم ثابت‫.‫ فيه نوع تاني مفصل أكتر بنسميه

 

Local symmetries

 

والفرق بينه وبين الجلوبال إن المعامل a ده مش بالضرورة يكون ثابت لكن يكون دالة في المسافة وفي الزمن ‫، يعني لو غيرت مكان نقطة في الزمكان النقطة إلي جنبها مش بتتغير فورياً لكن بتاخد وقت علشان تتغير وهكذا يبقي التغيير كأنه تأثير بينتشر في الفراغ بس مش فورياً.‫ 

 

https://www.facebook.com/moataz.emam.007/posts/pfbid0SZRaQaxbp8CT7RaGEgAzY2GfdBL5Y4jvt8pL3QiNyvZVhkw7Hn8Y2zopa9Ko5ka5l 

 

*********************************************************************************

 6-30-2022

تعالوا نتكلم عن السمترية -الجزء التاني

 

من أنواع السمترية الزمكانية النوع إلي بيخلط بين المكان والزمان ‫، يعني تيجي تحرك الحاجة في المكان تتحرك في الزمان‫.‫ وعلي فكرة ناس كتير مش عارفة إن ده بيحصل في الفيزيا الكلاسيكية‫.‫ يعني مش محتاج نسبية ولا حاجة‫.‫ إلي بنسميها تحويلات جاليليو تعتبر نوع من السمترية‫.‫ هي معادلاتها سهلة وأي حد درس سنة أولي عارفها‫.‫ لكن نقدر نقول إنها سمترية زمكانية تقريبية‫.‫ لكن لما نيجي نخش في النسبية ونعمم تحويلات جاليليو بتحويلات لورتنز تصبح سمترية زمكانية حقيقية‫.‫ لأن في النسبية بيتضح لينا إن إحنا عايشين في زمكان رباعي الأبعاد ‫، وأن القيم الفيزيائية بتاعتنا ‫، زي السرعات والمجالات وكدة عبارة عن متجهات وتنسورات في أربع أبعاد‫.‫ لما تلف فهي بتلف في الأربع أبعاد وتحافظ علي طولها في الزمكان‫.‫

 

التفاصيل مش مهمة مش عايزك تنام مني ‫، المهم إنها سمترية زمكانية رباعية الأبعاد تقدر تعتبرها تعميم للسمترية الدورانية في تلات أبعاد إلي إتكلمنا فيها المرة إلي فاتت‫.‫ يعني بدل ماتدور الشيء في تلات أبعاد بتدوره في أربعة ‫، يطلع زي ماهو ‫، سمترية أهي!‏

تعالوا بقي نحط قاعدة ‫، السمتريات أحياناً بيتم جدولتها بإستخدام نظرية في الرياضيات إسمها group theory ‫، نظرية المجموعات ‫، وهي النظرية إلي بتحط أسس للسمتريات المختلفة‫.‫ يعني بتقسم الكميات المختلفة لمجموعات ليها خواص متشابهة بشروط إن يكون كل مجموعة ليها أسس للجمع والطرح والضرب‫.‫ وممكن تبقي المجموعة الواحدة محتواها أرقام صحيحة أو أرقام حقيقية أو تخيلية أو كواترونية أو مصفوفات وهكذا‫.‫ ويكون فيه قاعدة إن حاصل جمع أو ضرب أي عضوين في المجموعة يدي عضو في نفس المجموعة‫.‫

علي سبيل المثال ‫، المصفوفة matrix للي دارسين رياضيات عارفين إنها كمية من أرقام مختلفة بتحول شيء لشيء تاني‫.‫ إمسك مثلا مصفوفة الدوران ‫، إلي لما تضربها في كمية معينة تخليها تدور في الفراغ ‫، زي الدوران إلي إتكلمنا عنه في الجزء الأول‫.‫ كل مصفوفة دورانية هي جزء من مجموعة الدوران إلي بتوع الرياضيات بيسموها R(3) يعني دوران Rotation في تلات أبعاد‫.‫ إمسك قلم رصاص مثلا وحطه علي الترابيزة في إتجاه الشمال‫.‫ علشان تدوره للشرق محتاج تشتغل عليه بمصفوفة دوران ‫، وعلشان يلف للجنوب إشتغل عليه بمصفوفة تانية ‫، وممكن تختصر الطريق وتضرب المصفوفتين ببعض تطلعلك مصفوفة تالتة تدوره من الشمال للجنوب مباشرة‫.‫ كل المصفوفات دي أعضاء في المجموعة R(3)‫‫ ‫

 

السمتريات الزمكانية ليها مجموعات برضه‫.‫ تحويلات جاليليو بتعمل Galilean group , تحويلات لورنتز بتاعة النسبية العامة ليها Lorentz group

 

وتقدر تجمع كل السمتريات إلي إتكلمنا عنها‫

Spatial translation symmetry

Time translation symmetry

Lorentz transformations

كلهم مع بعض أعضاء في مجموعة إسمها 

 

Poincare group

 

يعني لو عندك كمية فيزيائية عايزة تنقلها في الفراغ وفي الزمان وتدورها في الفراغ وتدورها في الزمكان ‫(‫يعني تخليها تتحرك بسرعة ثابتة‫)‫ يبقي الكمية إلي إنت محتاجلها حتلاقيها عضو من أعضاء مجموعة پوينكاريه دي‫.‫

شوف الصور لبعض التفاصيل إلي حيتعرف عليها إلي درسوا شوية نسبية‫.‫

 

مصدر الصور‫: كتابي

 

 https://www.facebook.com/moataz.emam.007/posts/pfbid02wLNYxXvHj9tcAtkg64Hn79AZmLP4BX5K5byvje9oU7XMmivj3RWnuH6nyYrDmTD4l

 

*********************************************************************************

6-13-2022

 

تعالوا نتكلم عن السمترية -الجزء التالت

 

إتكلمنا قبل كدة عن السمتريات الزمكانية ‫، إلي أي حد يقدر يتخيلها‫.‫ فيه أنواع تانية بيسموها سمتريات داخلية 

 

Internal symmetries

 

لأنها بتبقي مدفونة جوة الرياضيات ماتقدرش تتخيلها كسمترية مكانية أو زمانية‫‫.‫ لكن تعريف السمترية إلي إتكلمنا عنه في الجزء الأولاني ينطبق عليها‫‫:‫ إنها تغيير في المعادلات لا يؤثر في النتيجة الفيزيائية‫.‫

من السمتريات دي نوع مهم قوي إسمه

 

gauge symmetry

 

الله لوحده أعلم ترجمتها إيه بصراحة‫.‫ خلينا نقول سمترية الجيدج بتعطيش الجيم التانية بالمصري (الغيدج عند اخوانا الشوام)‫.‫ إيه بقي البتاعة دي‫‫؟ وإيه أهميتها‫؟

 

علشان أشرحلك النقطة دي خليني المرادي أشرحلك بس يعني إيه نظريات المجالات

 

field theories

 

والمرة الجاية أشرحلك سمترية الجيدج‫.‫ نظريات المجال دي هي النظريات إلي بتصف المجالات المختلفة ‫، يعني مثلاً المجال الكهرومغناطيسي كمثال واضح كلنا عارفينه واحدة منها‫.‫ وبتنقسم النظريات دي لأنواع ‫زي المجالات العددية

 

scalar fields

 

إلي بتقول إن الفضاء مليان بمجال ماليه كله من أوله لأخره بحيث إنه في كل نقطة في الفضاء المجال ممكن قياسه برقم واحد محدد‫.‫ مثال مشهور مثلاً مجال الحرارة‫.‫ الحرارة في الغرفة إلي إنت فيها مثلاً بتتغير من نقطة لنقطة‫.‫ أكيد أدفا جنب الدفاية وأبرد جنب التكييف‫.‫ لكن كل نقطة في فراغ الغرفة المجال ‫(‫إلي هو الحرارة في مثالنا ده‫)‫ بيتوصف برقم واحد محدد إلي هو درجة الحرارة‫.‫ أول صورة فيها تمثيل لمجالات الحرارة علي سطح الأرض مثلاً‫.‫

 

وفيه مجالات متجهية

 

vector fields

 

إلي بتوصف مجال لازم ليه إتجاه بالإضافة للرقم إلي بيوصفه‫.‫ كمثال بسيط مجال سرعة المية في البحر أو في نهر‫.‫ كل نقطة في المية بتتحرك بسرعة في إتجاه محدد وبتتغير القيم والإتجاهات بحسب مكان النقطة‫. يعني كل نقطة في الفراغ ليها رقم ‫، إلي هو السرعة ‫، وإتجاه إلي هو إتجاه الحركة‫.‫‫ تاني صورة فيها تمثيل لمجال متجهي.‫

 

وفيه كمان حاجة إسمها مجالات تنسورية بس دي شرحها يطول‫.‫ المهم أعتقد وصلتك الفكرة‫.‫ خليك معايا ‫، الپوست إلي جاي حييجي بسرعة‫.‫

مصادر الصور‫:

https://www.forbes.com/.../ask-ethan-what-is-a-scalar.../...

https://math.stackexchange.com/questions/439228/how-to-construct-a-vector-field-under-these-conditions

 

 

 

https://www.facebook.com/moataz.emam.007/posts/pfbid06Va9rkkQBR8WrDvbkK6Mm7qVzLEJo2dFCEkqTih9q18AdvLtXR8JWBn154w9b4oBl

*********************************************************************************

6-14-2022

 

تعالوا نتكلم عن السمترية -الجزء الرابع

 

المجالات إلي عرفناها المرة إلي فاتت تنقسم لأنواع ‫، والأنواع دي بتعتمد علي موضوع سمترية الجيدج إلي عايزين نعرفها هنا‫.‫ إزاي‫؟ كالأتي‫: كل نظرية من النظريات دي بيبقي ليها حاجتين مهمين بيوصفوها‫:

 

Potential and field strength

 

إلپوتنشيال وقوة المجال‫.‫ يعني حديك مثال بسيط خالص من فيزيا ثانوي‫.‫

تخيل طاقة الوضع بتاعة الجاذبية

 

U=mgy

 

لجسم له كتلة m وعلي إرتفاع y من سطح الأرض‫ ‫، و g هو التسارع بتاع الجاذبية.‫

دي ينشأ عنها قوة الجاذبية علي الجسم بإنك تاخد سالب تفاضل U بالنسبة لy فتحصل علي‫:

 

F=-mg

 

إلي هو الوزن بتاع الكتلة m ‫.‫

طيب تعال نقسم الناحيتين علي m ‫يطلعلك 

 

V=U/m

 

إلي ممكن نسميها پوتنشيال الجاذبية ‫، وهي طاقة الوضع لكل كجم‫:

 

V=gy

 

أما القوة فتصبح قوة لكل كجم إلي ممكن نسميها مجال الجاذبية نفسه

 

E=F/m=-g

 

ونفس الشيء بيحصل في الكهربا الإستاتيكية مثلا ‫، بس ساعتها الپوتنشيال هو إلي بنسميه الڤولت بتاع المجال‫.‫

المهم كدة فهمنا إن عندنا حاجتين‫: الپوتنشيال ‫، وقوة المجال نفسه‫.‫ أو طاقة الوضع والقوة المؤثرة‫.‫

طيب تخيل معايا في المثال أعلاه إننا غيرنا الإرتفاع y بدل ما بقي من سطح الأرض بقي من سطح الترابيزة مثلا ‫، يعني جمعنا عليه إرتفاع ثابت h

 

V=g(y+h)

 

لاحظ إنك لما تاخد التفاضل علشان تحصل علي قوة المجال تديك نفس النتيجة

 

E=-g

 

محصلش أي تغيير!‏!‏ لأن تفاضل أي رقم ثابت بصفر!‏!‏!‏ ودي حاجة أي طالب فيزيا في ثانوي عارفها ‫، إن طاقة الوضع بتعتمد علي الإرتفاع y أياً كان الإرتفاع ده من أي حتة وحتديك نفس المجال ونفس القوة ولن يتغير شيء!‏

 

الله!‏ دي سمترية يا معلم!‏!‏

 

لأن تعريف السمترية هو إنها عملية رياضية لما تعملها في المعادلات تديك نفس النتيجة الفيزيائية‫.‫ العملية الرياضية هنا هي جمع الرقم الثابت h والنتيجة الفيزيائية إن المجال E وبالتالي القوة F طلعوا زي ما هم من غير تغيير‫.‫

 

هي دي الجيدج سيمتري‫.‫ أو بالأصح ده يمكن أبسط مثال ممكن للجيدج سيمتري‫.‫ هي ببساطة إنك تعمل حاجة في الپوتنشيال ويطلعلك نفس المجال هو هو‫ وبالتالي نفس القوي المؤثرة إلي سيادتك بتشوفها في المعمل.‫

 

تلاقي بقي كل نظريات المجالات بتاعتنا مهما كانت معقدة كلها فيها هذا النوع من السيمتري ‫، بس العملية الرياضية إلي تعملها بتكون أكتر تعقيداً من مجرد إضافة رقم‫.‫ والجماعة بتوع الرياضيات بيلاقوا

 

groups

 

لتعريف كل نوع من أنواع السمتريات دي‫.‫ زي ما لقوا جروپات پوانكاريه ولورنتز إلي إتكلمنا عنها في الجزء التاني‫.‫ لكن بيبقي ليها تصنيفات مختلفة وأسماء أكتر تعقيداً‫.‫

 

مثلاً مثلاً يعني نظرية ماكسويل الكهرومغناطيسية السمترية بتاعتها تنتمي للجروپ

 

U(1)

 

إلي هي إختصار 

 

The Unitary group of degree one

 

والنظريات التانية إلي بتحكم مثلاً القوي النووية القوية 

 

Strong Nuclear Force

 

تنتمي لجروپ 

 

SU(3)

Special Unitary Group of degree three

 

وأخيراً نظرية 

 

Electroweek theory

 

إلي بتوحد الكهرومغناطيسية مع القوة النووية الضعيفة تعتمد علي إدماج جروپين ‫، الأولاني هو U(1) بتاع الكهرومغناطيسية ‫، والتاني SU(2)

 

علشان كدة بنقول إن نظرية الإلكتروويك تخضع للجيدج سيمتري

 

SU(2) x U(1)

 

كدة بقي نقدر نقول إن تلاتة من القوي الأربعة للطبيعة ‫، إلي هم الكهرومغناطيسية والنووية القوية والنووية الضعيفة بيتوصفوا بنموذج واحد ليه سمترية

 

U(1) × SU(2) × SU(3)

 

ده الي بنسميه النموذج المعياري او

 

Standard Model of Particlr Physics 

 

والقوة الرابعة ‫، إلي هي الجاذبية ‫، بتخضع لجروپ مختلف حنتكلم عنه بعدين‫.‫

 

فلما حضرتك بقي تكون عايز توصف واحدة من النظريات دي تقدر تعتمد علي تصنيفة الجروپات دي‫.‫ يعني لو بتتكلم مع واحد صاحبك مثلاً وعايز تقوله ‫"‫النظرية الكهرومغناطيسية‫"‫ يكفي إنك تقول 

 

The U(1) Gauge Theory

 

وهو حيعرف قصدك إيه ‫(‫أو ممكن ما يعرفش وإنت بتقول كدة بس علشان تتنطط عليه بمصطلحات مايفهمهاش وتبان إنك واد فتك قوي‫)‫‫.‫

 

طيب إيه أهمية الموضوع ده‫؟

 

ليها أهميات كتيرة بس من أهمها إنك تقدر تستعملها علشان تدور علي نظريات أكبر وأشمل منها‫.‫ يعني تشتغل بالعكس‫.‫ تقول مثلاً إيه‫.‫ أنا عايز ألاقي نظرية تكون بتجمع القوي التلاتة في بعض ‫، بدل ما تدور علي النظرية دي بإستخدام الأكشن مثلاً ‫(‫شوف پوستات قديمة ليا بتشرح يعني إيه أكشن‫)‫ تقدر ببساطة تروح للجماعة بتوع الرياضيات وتقولهم‫: إيه المجموعات الأعلي من 

 

U(1) × SU(2) × SU(3)

 

لكن تحتوي الجروپات التلاتة دول جواها‫؟

 

يقولولك مثلا إن الجروپ SU(5) أو SO(10) أو E6 دي كلها جروپات أكبر من 

 

U(1) × SU(2) × SU(3)

 

لكن تحتوي الجروپات 

 

U(1) × SU(2) × SU(3)

 

جواها كحالة خاصة ‫، تروح إنت بقي واخد الجروپات الجديدة دي وتبني منها نظرية فيزيائية تكون نظرية محتملة لتوحيد القوي التلاتة‫؟

وضحت‫؟

 

أخر مثال حقولهولك هو نظرية الأوتار الفائقة ‫، فيه خمس نظريات للأوتار الفائقة ‫(‫شوف محاضراتي في الموضوع ده علي اليوتيوب‫)‫ ‫، واحدة منهم ليها جروپ جيدج إسمه

 

E8xE8

 

الجروپ ده جواه 

 

U(1) × SU(2) × SU(3)

 

وبيحتمل وجود الجراڤيتون كمان!‏ يعني النظرية دي تعتبر نظرية محتملة لتوحيد القوي الأربعة كلها مع بعض‫.‫

مصدر الصورة‫:

 

https://acelerandolaciencia.wordpress.com/2014/01/24/a-quick-look-at-the-standard-model-of-particle-physics/

 

 

 

https://www.facebook.com/moataz.emam.007/posts/pfbid02x91FR5C491Vmo8SKbtphTPxDuBYoEh9PQN7xuBDHC8JXAwvCCYRD3TYUfahZFM48l 

 

*********************************************************************************

6-15-2022

 

تعالوا نتكلم عن السمترية -الجزء الخامس 

 

السمتريات إلي إتكلمنا عنها قبل كدة كلها سمتريات يا إما خاصة بالنسبية الخاصة يا إما خاصة بنظريات المجال‫.‫ وكلها سمتريات بتفضل موجودة معانا حتي لما بِنُجَوِز النسبية الخاصة بنظرية المجال ومع ميكانيكا الكم ويطلعلنا نظريات المجال الكمومي

 

Quantum field theories

 

إلي بتكون العامود الفقري للنموذج المعياري 

 

The Standard Model

 

وبنعتبرها أنجح نظريات في الفيزياء علي الإطلاق‫.‫ وفيه سمتريات تانية تنطبق برضه علي النموذج المعياري ‫، زي مثلاً حاجة إسمها CPT سيمتري‫.‫ وفيه كمان حالات إنكسار السمترية ‫، Spontaneous symmetry breaking وهي الحالات إلي السمترية فيها تنكسر تحت ظروف معينة‫.‫ مش حتكلم علي الحالتين دول لأنهم حيحتاجوا تحضير أكبر بكتير من إلي المكان والزمان يسمحله‫.‫ إحنا عموماً بنتكلم عن أمثلة علشان الصورة العامة توصل‫.‫

 

بس فيه سمتريات لازم أكلمك عنهم لأنهم بيغطوا نظريات تانية في الفيزياء ‫، مثلاً إيه السمترية بتاعة النسبية العامة‫؟ إذا كان الستاندارد موديل بكل سمترياته المذكورة هو أحد أعمدة الفيزياء الأساسية فالنسبية العامة هي العامود التاني‫.‫ لازم ليها سمترية‫.‫

 

الحقيقة أه ‫، ليها كذا سمترية مش واحدة بس‫.‫ لكن أنا النهاردة حركز علي أهم سمترية فيهم ‫، سمترية عجيبة جداً ‫، وفي نفس الوقت سمترية نقدر نقول إنها تنطبق أيضاً علي كل النظريات التانية في الفيزياء‫.‫ سمترية بتحكم الميكانيكا الكلاسيكية ‫، ونظريات المجال والنسبية العامة ‫، ونظريات المجال جوة النسبية العامة ‫، وبتحكم نظرية الأوتار وكل محاولات تكميم الجاذبية‫.‫ سمترية لو عرفتها حتستغربها جداً لكنها من القوة بحيث نقدر نقول إنها سمترية حاكمة لكل الفيزياء ولكل الكون‫.‫ من كتر قوة السمترية دي أنا إخترتها لتكون الأساس إلي بنيت عليه طريقتي في تدريس الفيزياء إلي وضحتها في كتابي ‫، بل إن عنوان الكتاب نفسه فيه إسم السمترية ‫(‫‫Covariant Physics)‫‫.‫ إسمها

 

The Principle of Covariance

 

‫وهي حالة خاصة من سمترية رياضية إسمها لامتغيرة الديفيومورفيزم

 

Diffeomorphism invariance

 

وليها جروپات زي السمتريات التانية وكل حاجة‫.‫ بس خلينا نشرحها بصورة بسيطة‫.‫

 

سمترية الكوڤاريانس هي الفكرة البسيطة إن كتابة قوانين الفيزياء في أي نظام إحداثيات لازم يديك نفس النتيجة الفيزيائية ‫، يعني نفس الفيزياء لكل مراقب‫.‫ تكتب قوانين الفيزياء في الإحداثيات الكارتيزية ولا في الإحداثيات الكروية أو إحداثيات متحركة قصورية أو غير قصورية أو أي إحداثيات لازم يديك نفس القوانين هي هي ونفس النتيجة الفيزيائية هي هي‫‫.‫ دي مش بس فكرة بسيطة ‫، لأ دي كمان بديهية ومنطقي‫ة.‫ وتنطبق علي كل قوانين الطبيعة من ميكانيكا نيوتن ‫، لكهرومغناطيسية ماكسويل ‫، لنظريات المجال كلها‫.‫

لكن النسبية العامة تحديداً بتعتمد علي فكرة ال

 

General Covariance

 

إلي هي حالة قصوي من سمترية الكوڤاريانس المشروحة أعلاه‫.‫ الفكرة إن أي قانون فيزيائي في النسبية العامة لازم يكون ليه ‫"‫لامتغيرات‫"‫

 

Invariants

 

وهي كميات لا تتغير ولا تختلف من نظام إحداثيات لنظام إحداثيات تاني ‫، بمعني أخر كل المراقبين حيتفقوا علي قيمتها حتي لو كانوا موجودين في إحداثيات مختلفة‫ ‫(‫‫متحركة أو متعجلة)‫.‫ من أهم هذه اللا متغيرات إلي بنسميه المتريك

 

Metric

 

وهو رقم‫ ‫، تقدر تعتبره تعميم لنظرية فيثاغورس في أربعة أبعاد وقد تكون منحنية‫.‫ ‫(‫شوف پوستات سابقة عن معني المتريك بتفصيل أكتر‫)‫‫.‫ أي مراقب في النسبية العامة ‫، أياً كانت إحداثياته وأياً كان موقعه حيشوف القيمة الرقمية للمتريك زي أي مراقب أخر‫.‫ والكلام ده ينطبق علي لامتغيرات تانية في النسبية العامة كمان‫.‫ لكن المفاجأة إنها كلها بتعتمد علي المتريك‫.‫ يعني خلينا نقول إن حقيقة عدم تغير المتريك لأي مراقب ‫(‫‫general covariance)‫ هي الأساس المرجعي إلي تقدر تبني عليه النسبية العامة كلها‫. خلي بالك بنتكلم عن اي مراقب حتي لو كان في اطار مرجعي غير قصوري ، يعني بيتسارع. 

 

الفكرة دي مهمة جداً ‫لأن تطبيقاتها كتيرة ، مقارنة المتريك من مراقب لمراقب هي إلي بتخلينا نقدر نستنتج حاجات زي مثلاً إختلاف مرور الزمن بالنسبة لمراقبين مختلفين ‫، أو إختلاف أطوال من مراقب لمراقب وهكذا ‫، ودي حاجات أساسية في النسبية العامة‫.‫ ونقدر نطلع معادلات الخطوط الجيوديسية وحركة الأفلاك ‫، كل ده بمقارنة المتريك إعتماداً علي سمترية الكوڤاريانس‫.‫

 

الموضوع ده كبير ‫، وزي ما قلت أنا شخصياً بحب السمترية دي جداً ‫، وشايف إنها مفهوم أساسي تقدر تدرس بيه الفيزياء من أولها لأخرها‫.‫ وطبقت الفكرة دي في كتابي من أوله لأخره‫.‫ بمعني إني في كتابي إستعرضت كيف أن كل الفيزياء من أيام جاليليو لحد الأبحاث إلي طالعة أول إمبارح ينطبق عليها مبدأ الكوڤاريانس‫.‫ بس بدرجات مختلفة ‫، فتلاقي ال Classical covariance و Special Covariance لحد ما توصل للGeneral Covariance إلي يديك النسبية العامة‫.‫ حعمل إعلان وأحط جدول محتوي الكتاب‫.‫

 

 

https://www.facebook.com/moataz.emam.007/posts/pfbid0s672CjtfgiGCZmMDzG2NYbriTQvEvhZFbPTTBGVesJQUk5b2iyczWCRxBBPWYZaZl

 

 *********************************************************************************

  6-18-2022

تعالوا نتكلم عن السمترية - الجزء السادس 

 

ححكيلكوا النهاردة عن نوع من السمترية قليلين قوي إلي سمعوا عنه ‫، وبالرغم من كدة فهو موجود تقريباً في كل فروع الفيزيا‫.‫ أه زيه زي سمترية الكوڤاريانس إلي إتكلمنا عنها المرة إلي فاتت ‫، لكن الفرق إنه سمترية غريبة ومش بديهية ‫، بل بالعكس يمكن محدش فاهم لحد النهاردة هي ليه موجودة بكثرة في معظم نظرياتنا‫.‫ موجودة في ميكانيكا نيوتن وموجودة في كهرومغناطيسية ماكسويل ‫، دانت كمان تلاقيها في الأوتار الفائقة‫.‫ 

 

السمترية دي إسمها السمترية السمپلكتيكية

 

Symplectic symmetry

 

إسم غريب ويخض!‏ إيه الحكاية بقي‫؟

 

عندك متجه ‫، متجه عادي خالص vector ‫ثنائي الأبعاد في فضاء إقليدي عادي ‫، يعني علي ورقة مسطحة عادية‫.‫ إحنا بِنعَرف الفضاء ده بإستخدام نوعين من التحويلات ‫، أولاً إل Identity إلي هي مصفوفة لما تضربها في المتجه تديك نفس المتجه ولا كأنك عملت حاجة‫.‫ تاني تحويل هو تحويل الدوران ‫، زي إلي إتكلمنا عنه في الجزء التاني‫.‫ لما تضرب المتجه في تحويل دوران يلف في الفراغ بس بشرط إن نتيجة ضرب متجهين تفضل تديك نفس النتيجة حتي لو دورت المتجهين مع بعض بنفس الزاوية‫.‫ كل ده كلام بديهي وأي طالب سنة أولي فاهم الكلام ده‫.‫ التحويلات إلي بتحقق الدوران مع الحفاظ علي نتيجة الضرب بتكون مجموعة group زي ما قلنا قبل كدة ‫، وفي المثال ده بالذات المجموعة إسمها R(2) يعني الدوران في بعدين‫.‫ ودي سمترية زي ما شرحنا قبل كدة‫.‫

 

طيب تخيل فضاء معين ‫، مش فضاء عادي لكن فضاء رياضي ‫، الIdentity تختلف عن الIdentity العادية زي ما باين في الصورة ‫، بتبقي مصفوفة مختلفة إسمها Symplectic Matrix ‫، زي مانت شايف الوحايد بتبدل مكانها مع الأصفار وواحد فيهم بياخد علامة سالب‫.‫ نتيجة كدة الضرب بين متجهين بيبقي Antisymmetric مش symmetric ‫.‫ التحويلات بقي إلي تحقق إن الضرب يفضل يدي نفس النتيجة ماهياش تحويلات دورانية لكنها تحويلات symplectic ودي بتعمل group إسمه The Symplectic Group. في المثال ده Sp(2) .

 

إيه يا عم معتز الرغي ده‫.‫ أنا تهت منك!‏!‏ معقول البتاع المكلكع ده موجود في الفيزيا‫‫؟ وكل الفيزيا زي مانت بتقول‫؟ 

 

أه والله موجود ‫، ده كمان موجود في ميكانيكا نيوتن‫.‫‫ لو عملت متجهات مكوناتها هي إحداثيات المكان q والزخم p بتاع نظام ميكانيكي المتجهات دي بتطلع قابلة للتحويل تحت الSymplectic Transformations. طيب نتعرف عليها إزاي في ميكانيكا نيوتن‫؟ هي مش بتبان في قوانين نيوتن نفسها لكن تبان في قوانين هاميلتون إلي بعضكم درسوها‫.‫ بتبان إزاي‫؟ بص علي معادلات هاملتون في الصورة التانية‫.‫ لو كنت درستها تبقي عارفها كويس‫.‫ شايف المعادلتين شبه بعض إزاي‫؟ تقريباً حاجة واحدة ‫، لكن الفرق فقط في علامة السالب في المعادلة التانية!‏!‏!‏ دي العلامة يا مارد!‏!‏ الإشارة إن الفضاء إلي فيه الcoordinates q والزخم p هو فضاء سيمپلكتيكي ‫، يحكمه ال Symplectic group.

 

مش بس كدة ‫، دي معادلات ماكسويل كمان في الفضاء ده‫.‫ شايفها في الصورة‫؟ شايف الشبه بين المعادلات‫؟ شايف علامة السالب‫؟ ده معناها إن المجال الكهربي والمجال المغناطيسي بيعملوا سوا متجه في فضاء سيمپلكتيكي‫.‫ 

 

أيوة أيوة أنا فاهمك يالي درست معادلات ماكسويل قبل كدة‫.‫ شايفك وإنت بتقول دي معادلات ماكسويل من غير شحنات وتيارات كهربية‫.‫ أه معاك حق ‫، فعلاً ده صحيح ‫، وجود الشحنات والتيارات الكهربية في معادلات ماكسويل بيبوظ السمترية السمپلكتيكية‫.‫ طيب خلاص كدة ده معناها إن معادلات ماكسويل الكاملة لا تخضع للسمترية دي صح‫؟ أه صح بس إيه رأيك بقي إنها ممكن ترجع تخضع للسمترية السمپلكتيكية دي لو فيه أحاديات أقطاب مغناطيسية‫؟ Magnetic Monopoles!! 

 

يا راجل!‏ يعني وجود المونوپولز يرجع معادلات ماكسويل للسمترية السمپلكتيكية دي‫؟ أيوة يا فندم‫.‫ الله طيب ما تلاقوها بقي خلينا نخلص‫.‫ للأسف مش لاقينها بس صدقني وجود المونوپولز دي يحل مشاكل كتير في الفيزيا‫ مش بس مشكلة السمترية‫.‫ نبقي نفردلها پوستات لوحدها ‫(‫المونوپولز كان رسالتي في الماجستير‫)‫‫.‫

 

بس يا سيدي أدي السمترية السمپلكتيكية‫.‫

 

طيب هل فيه نظريات تانية في الفيزيا بتظهر فيها السمترية دي‫‫؟

 

أماااااال‫.‫ إنت دور بس حتلاقيها بتطلع في حتت غريبة في الoptics وفي بعض نظريات solid state وكمان كتير من نظريات الأوتار الفائقة والسوپرجراڤيتي‫.‫ الموضوع ده من المواضيع إلي شدتني أنا شخصياً جداً وإشتغلت فيها في بعض أبحاثي‫.‫

.‫

مصدر الصور‫: الصورة الأولي بحث ليا في Symplectic covariance https://arxiv.org/abs/0904.1951

الصورة التانية كتاب جولدشتاين في الميكانيكا الكلاسيكية وكتابي‫.‫

 

https://www.facebook.com/moataz.emam.007/posts/pfbid0MLUYWPKnWtAV39uGpNW1sM5qpKmYC7cvagy225dkcTHxD1Kcy7cj1tQFnviquKkHl 

 

*********************************************************************************